Comment faire un rubik's cube 4x4

Comment faire leRubik’s Cube 4x4? Vous vous êtes sûrement déjà demandé comment un cube est résolu 4x4. Dans ce tutoriel, nous allons l’expliquer étape par étape mais, pour cela, il est nécessaire que vous ayez d’abord appris à faire le rubik’s cube 3x3. Si vous avez besoin d’aide, vous pouvez consulter notre tutoriel.

Savez-vous déjà comment faire le cube 3x3 et voulez-vous faire face à de nouveaux défis? Le rubik’s cube 4x4 est le prochain en difficulté. Le résoudre est un peu plus compliqué que le 3x3, car vous devrez apprendre de nouveaux algorithmes, mais ne vous inquiétez pas, nous les expliquerons en détail.

Pour arriver à la solution de ce cube, nous utiliserons la méthode de réduction, c’est-à-dire que nous réduirons la 4x4 d’un 3x3. Pour ce faire, nous allons d’abord faire les centres, puis les bords et, une fois que nous aurons atteint ce point, nous résoudrons les coins comme dans un 3x3. Cependant, nous rencontrerons de nouveaux problèmes, tels que les parités, mais tranquil@, avec notre aide, vous le résoudrez sans problèmes. C’est parti ! 

rubik’s cube 4x4 pièces

Comme le rubik’s cube 3x3, le cube 4x4 est également composé de centres, d’arêtes et de coins. Cependant, nous trouvons quelques différences: chaque centre est composé de 4 pièces, les bords par 2 et le coin ne sera qu’un. Au total, nous aurons:

• 24 pièces centrale
• 24 pièces qui composeront les 12 bords
• 8 coins

Centres cubes 4×4

Bords du cube 4×4

Coins cubes 4×4

Contrairement aux centres du cube 3x3, dans le 4x4 les centres ne sont pas fixes. Par conséquent, nous devons être très clairs sur leur position correcte afin de ne pas avoir de problèmes avec leur résolution.  

Faces du cube 4x4

Avez-vous remarqué la couleur des visages? De la même manière que dans le rubik’s cube 3x3 nous trouvons 6 couleurs, l’une en face de l’autre. L’opposé du blanc sera jaune; l’opposé du rouge l’orange et l’opposé du vert le bleu.

Rappelez-vous que, pour résoudre tout rubik’s cube nous devons toujours avoir un visage de référence qui, dans notre cas, sera blanc. De cette façon, si nous prenons le cube avec la face blanche vers le haut, la couleur qui reste à notre droite est le rouge, dont le contraire, comme nous l’avons mentionné précédemment, est l’orange.

C’est le schéma de couleurs standard et c’est celui que nous trouverons dans la plupart des cubes.

Notation pour rubik’s cube 4x4

Pour effectuer la rubik’s cube de 4x4 il faudra connaître une certaine notation, car il est fort probable que nous verrons des cas de parités qui seront résolus en appliquant certains algorithmes. Pour exécuter ces algorithmes, nous devons savoir ce que signifie chaque mouvement. Nous pouvons trouver:

• Les virages dans le sens inverse des aiguilles d’une montre : ce sont ceux qui seront contraires au fonctionnement de l’horloge.
• Virages dans le sens des aiguilles d’une montre : les virages que nous faisons selon les aiguilles de l’horloge.

Chaque lettre fait référence à un côté du cube, de sorte que :

• U (vers le haut) : couche supérieure
• D (vers le bas) : couche inférieure
• R (à droite) : calque droit
• L (à gauche) : calque gauche
• F (avant): couche avant
• B (Retour) : couche arrière

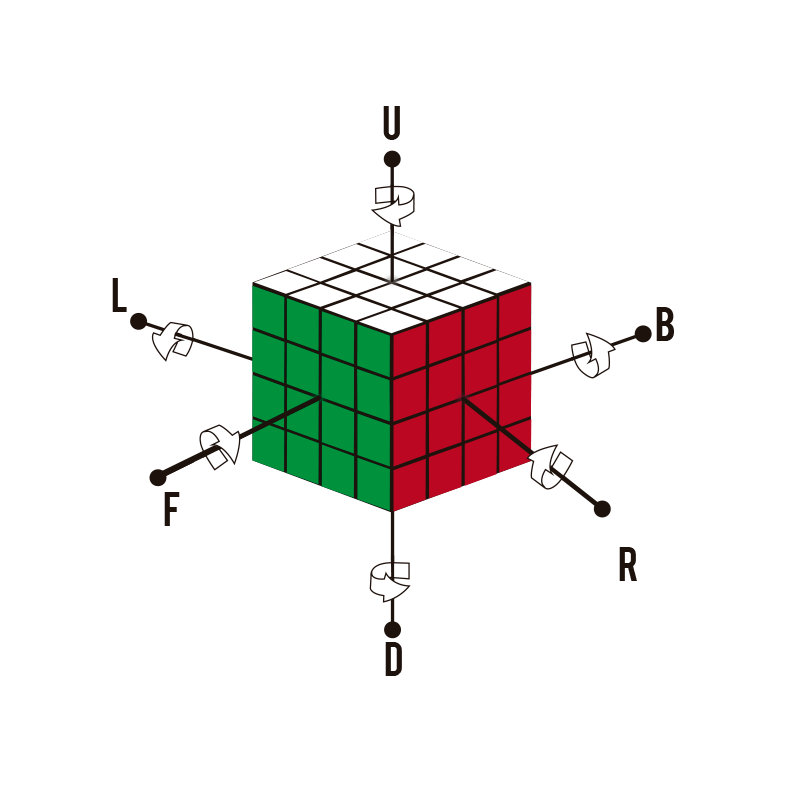
Virages dans le sens des aiguilles d’une

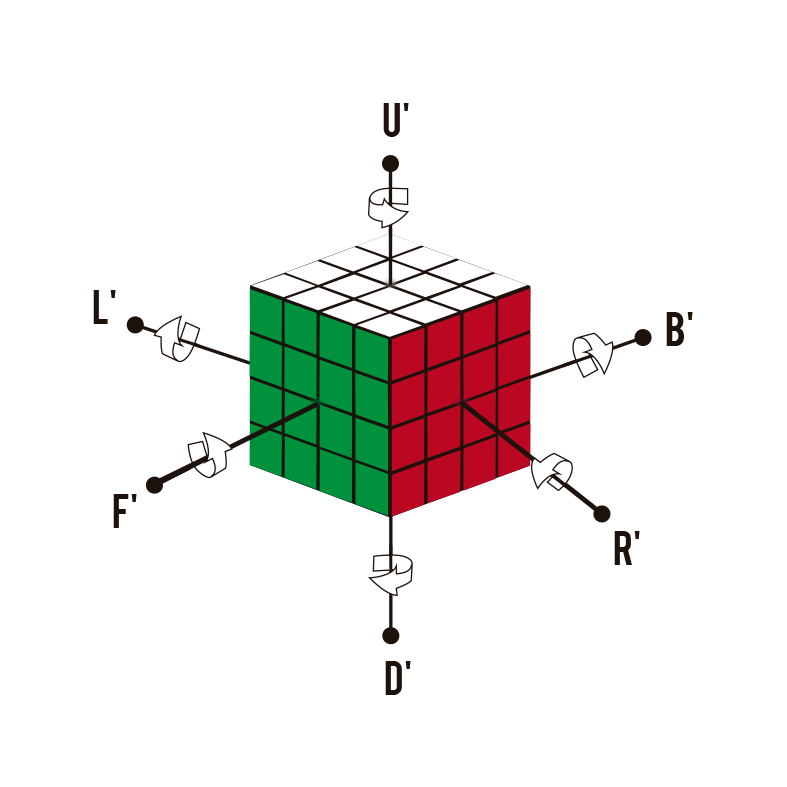
Virages dans le sens inverse des aiguilles d’une montre

Lorsque vous trouvez la lettre normale, c’est-à-dire sans apostrophe, cela signifie que celle qui tourne sera dans le sens des aiguilles d’une montre (U). Cependant, lorsqu’il porte l’apostrophe, il s’agit d’un virage dans le sens inverse des aiguilles d’une montre (U'). Si vous avez encore des doutes sur la notation, vous pouvez le résoudre dans notre article où nous expliquons toute la notation de la rubik’s cube. (Vous avez le lien un peu plus bas)

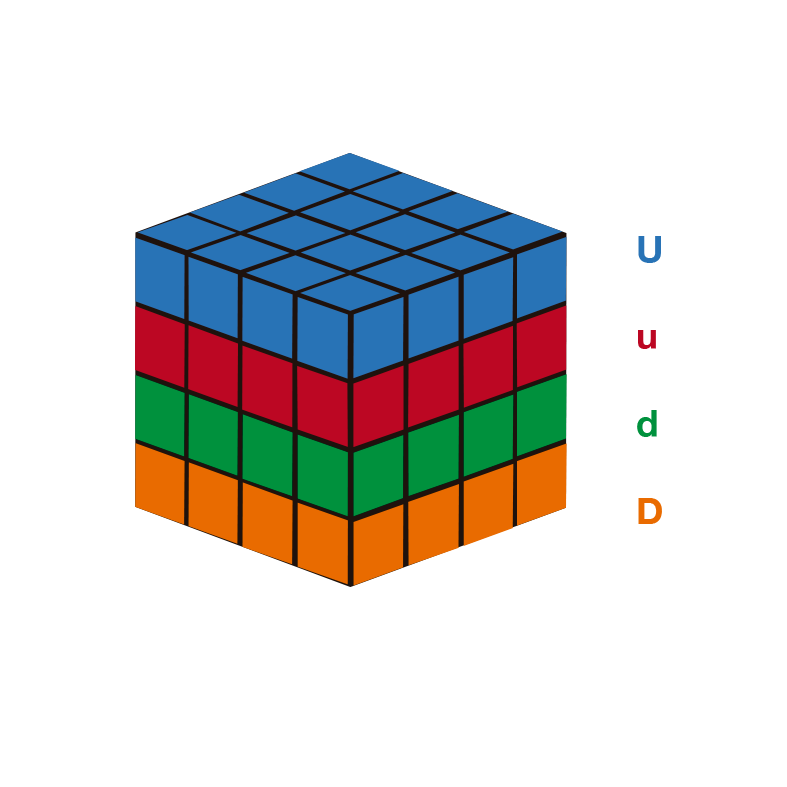
Rotations des couches internes du cube 4x4

Dans les cubes 4x4, en plus des virages temporels et dans le sens inverse des aiguilles d’une montre, il existe également des virages internes et des virages à deux couches. Pour indiquer la rotation des couches internes, nous mettrons la même lettre que pour la couche externe mais en minuscules.

Nous le montrons dans les illustrations suivantes:

Si c’est la première fois que vous voyez la notation du rubik’s cube 4x4 vous avez probablement besoin d’un peu plus d’informations sur les tours des calques. Dans le lien suivant, vous pouvez trouver toutes les informations en détail.

Étapes pour résoudre le rubik’s cube 4x4

Résoudre les centres

La première étape consistera à résoudre les centres du cube 4x4. Pour ce faire, nous oublierons le reste du cube car, les pièces centrales ne se déplaceront que dans les centres, c’est-à-dire qu’elles n’occuperont pas une autre position. Nous devrons regrouper les couleurs pour faire tous les centres. Nous devons prendre en compte, comme nous venons de l’expliquer dans la section précédente, la position des couleurs.

Pour faire les centres il n’y a pas d’algorithme spécifique, c’est fait par intuition. Ne désespérez pas, même s’il faut beaucoup de temps pour rassembler les pièces... vous finirez par y parvenir! Nous ferons des lignes de deux pièces de la même couleur et nous les placerons verticalement pour ne pas les casser lorsque nous tournons le cube. Regardons-le attentivement.

• Premier centre

Le premier centre que nous ferons sera le blanc.le plus simple à faire, puisque nous n’allons pas casser quoi que ce soit que nous avons déjà fait, ni le construire n’importe où en particulier. Dans cette étape, nous devrons simplement regrouper les quatre pièces centrales blanches. Pour ce faire, nous allons faire deux lignes blanches appariant les pièces deux par deux (tous les 2 pièces formeront une ligne) et nous les joindrons au même centre.

Maintenant, nous pouvons passer au prochain centre! Ne vous inquiétez pas, petit à petit vous prendrez de la pratique.

• Deuxième centre

Nous recommandons que le prochain centre que vous faites après le blanc soit son opposé, c’est-à-dire le jaune.

Pour résoudre ce centre, nous suivrons la même méthode que dans le centre précédent. Cependant, nous devons maintenant garder à l’esprit que, si nous faisons un mouvement qui modifie la pièces de la face blanche que nous avons mise précédemment, nous devrons récupérer ce virage après avoir fait correspondre les pièces que nous voulons joindre en formant une ligne. Par exemple, si je lève la face droite pour joindre deux pièces jaunes, après ce mouvement, je dois protéger les deux pièces que j’ai jointes et retourner le tour de la couche droite pour récupérer le centre blanc.

Par la suite, nous devons insérer la ligne au centre correspondant. Par exemple, nous avons une ligne jaune d’un côté et nous voulons l’élever du côté opposé du blanc. La première chose que nous devons faire est, avec le centre blanc ci-dessous, de mettre la ligne verticalement dans notre vue, de soulever le centre vers la couche supérieure, de protéger en faisant pivoter la couche deux fois et de renvoyer le premier mouvement. Vous le verrez plus clairement dans l’image suivante.

Ne vous inquiétez pas de la rotation des couches extérieures, elles ne détruiront pas ce que nous avons déjà fait.

Nous avons déjà la première ligne dans le centre opposé. Maintenant, nous allons faire la deuxième paire des couleurs et, pour l’élever, nous allons faire le même algorithme que dans la section précédente, mais nous allons le mettre sous la ligne que nous avons déjà faite (ligne par ligne), de sorte que lorsque nous tournons le calque supérieur deux fois et retournons le mouvement, le centre est terminé. Vous le verrez mieux dans l’image ci-dessous.

• Troisième centre

Une fois que nous avons fait les deux premiers centres, nous plaçons le cube sur le côté, de sorte que la couleur blanche et jaune, respectivement, reste à droite et à gauche.

Le troisième centre que nous faisons pourrait être n’importe qui. Celui que nous voyons que nous avons plus facile à construire. Si vous les trouvez tous difficiles, fixez-vous un objectif et oubliez le reste. Par exemple, commencez par le bleu. Associez deux pièces bleues, puis deux autres, de sorte que vous avez deux lignes; n’oubliez pas de mettre les lignes faites verticalement dans votre vue, afin de ne pas les casser lorsque vous tournez le cube. Par la suite, placez-les au même centre.

Nous n’avons toujours pas à nous soucier de la position des couleurs, c’est la première.

Pour cela il n’y a pas d’algorithmes, c’est de l’intuition simple. Ne vous inquiétez pas, avec de la pratique, vous verrez tout beaucoup plus facilement.

• Salle centrale

À ce stade, nous devons considérer la position des couleurs. Vous devez prendre en compte celui que vous avez construit pour placer les centres suivants dans leur position correcte. Par exemple, si vous avez construit le bleu, vous devez garder à l’esprit que, avec le blanc face vers le haut, à sa gauche va le rouge et à sa droite l’orange.

Dans ce cas, nous allons faire le centre rouge.

Nous remettons le cube de sorte que le centre blanc et jaune soit à droite et à gauche.

Nous recherchons deux pièces rouges afin de pouvoir faire une ligne. Ne vous inquiétez pas de la rotation des couches extérieures. Ils ne briseront rien de ce que nous avons fait, contrairement aux internes.

Nous faisons la première ligne et l’amenons à sa position correcte à côté de la couleur bleue. Nous expliquerons comment le faire plus en détail à la fin de ce paragraphe, mais en résumant: avec le centre blanc à notre droite et la ligne rouge à notre gauche, nous élevons la ligne bleue droite afin qu’il y ait un centre en dessous où se trouve la ligne rouge. Ensuite, nous tournons le calque où se trouve la ligne rouge, de sorte que sa position soit la ligne à côté de la ligne et renvoyons le centre bleu. Maintenant, nous aurons le centre bleu à nouveau construit et une ligne rouge dans sa position correcte.

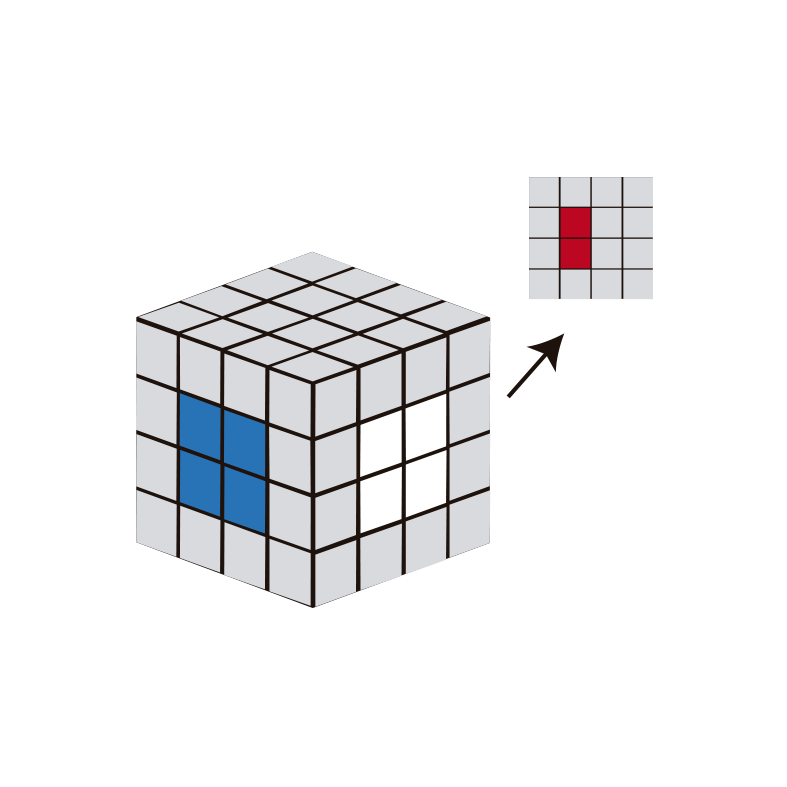
En plaçant les lignes au quatrième centre, nous pouvons trouver trois cas:  

• Premier cas : la ligne rouge est située au centre qui lui correspond. Tournez simplement le calque extérieur pour le laisser sur votre gauche et passez à l’étape suivante.
• Deuxième cas : la ligne rouge se trouve du côté opposé de la ligne bleue. Dans cette situation, l’algorithme à suivre serait (avec le centre blanc à notre droite):
  • Placez la ligne rouge sur votre gauche.
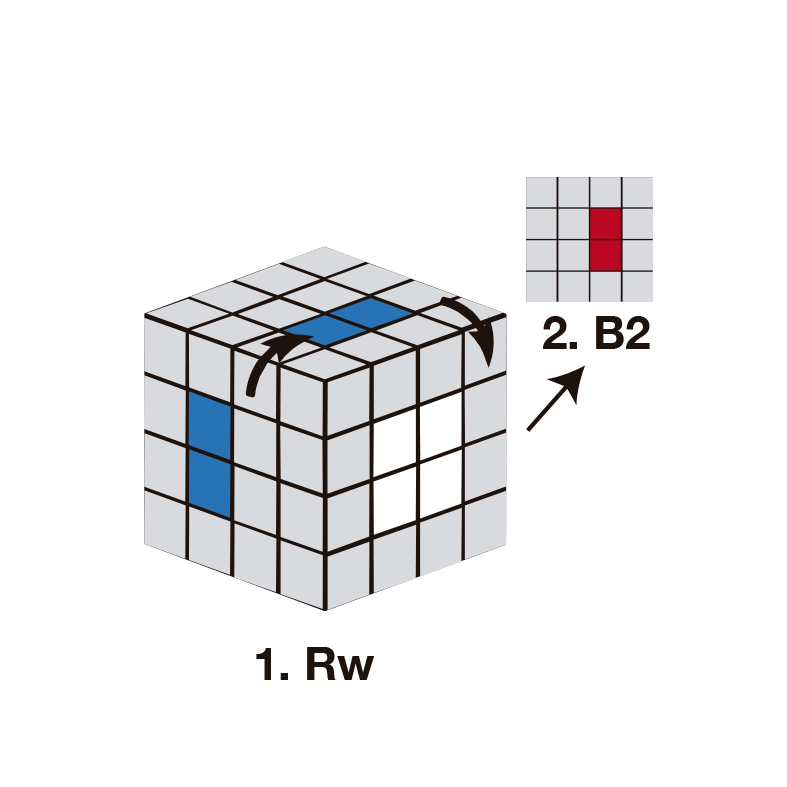
  • Effectuez l’algorithme : Rw, B2, Rw'. Où Rw grimpe la ligne bleue de droite un centre au-dessus; B2 fait pivoter la ligne rouge de gauche à droite, pour la placer à côté du bleu et Rw' renvoie le mouvement de la ligne bleue et abaisse à son tour la ligne rouge à sa position. Lorsqu’il est en son centre, tournez le calque où se trouve la ligne rouge pour le placer sur notre gauche (U2).

Si vous ne clarifiez pas comme ça, regardez l’image ci-dessous.

Troisième mouvement

Quatrième mouvement

• Troisième cas : si la ligne rouge est située à côté de la face bleue mais au centre qui correspond au centre orange, il faut faire le même algorithme que dans le cas précédent. Cependant, cette fois, au lieu de tourner la bonne couche une fois, nous le ferons deux fois. Rw2, B2, Rw2, U2.

Nous avons déjà la première ligne. C’est parti pour le prochain !

Pour placer la ligne manquante, nous ferons de même, en prenant soin de protéger et de renvoyer les mouvements qui impliquent la rupture d’un centre que nous avons fait. Une fois la ligne formée, nous utilisons l’algorithme que nous avons fait avec la première ligne.

Au cas où vous ne vous en souviendriez pas bien, nous vous rappelons à quoi ressemblait cet algorithme :

Avec le centre blanc sur notre droite: Nous plaçons la ligne rouge sur notre gauche dans le calque qui est, nous élevons la ligne droite bleue (une ou deux fois, selon l’endroit où se trouve la ligne rouge - il doit y avoir un centre sous notre ligne rouge -), nous tournons la couche de la ligne rouge deux fois pour qu’elle soit ligne avec ligne; et enfin, nous rendons le mouvement.

• Centres 5 et 6

Il ne nous reste plus que deux centres à faire. Pour résoudre les deux derniers centres, nous allons faire le vert et, par jeter, l’orange sera également faite. Remontez le moral, bientôt nous aurons le rubik’s cube 4x4 résolu!

Pour faire ce centre, nous allons d’abord faire une ligne verte, puis nous l’introduirons à côté du centre rouge. S’il est déjà placé dans sa position correcte, nous ferons comme avant: nous le mettons sur notre gauche et formons la prochaine rangée verte.

Cependant, nous constatons que c’est au centre qui correspond à l’orange, nous utilisons l’algorithme que nous connaissons déjà : Rw, B2, Rw'. En d’autres termes, avec le centre blanc sur notre droite et la ligne verte verticalement sur notre gauche, nous soulevons la couche droite une fois, tournons deux fois là où se trouve la ligne verte et retournons le premier mouvement. Une fois que nous l’avons fait, nous plaçons cette rangée sur notre gauche et faisons la ligne suivante.

Si nous ramenons la dernière ligne à sa position correcte la première ... génial, nous avons déjà résolu tous les centres!

Sinon, nous répéterons les mouvements précédents. Se souvenir. avec le centre blanc sur notre droite et la ligne verte verticale sur notre gauche, nous soulevons la couche droite une fois, tournons deux fois là où se trouve la ligne verte et retournons le premier mouvement. Visez bien l’algorithme : Rw, B2, Rw'.

Et... C’est tout! Nous avons déjà fait tous les centres. Voyons maintenant comment résoudre les bords.

Résoudre les arêtes

Cette étape est la plus compliquée, car nous retrouverons les parités redoutées qui caractérisent même les cubes, comme c’est le cas du rubik 4x4. Mais ne vous inquiétez pas, nous vous guiderons étape par étape afin que vous puissiez le résoudre.

Tout d’abord, pour faire les coins, il est très important que nous prenions en compte que nous les cherchions horizontalement, pas verticalement.

Notre premier objectif sera de trouver deux bords se faisant face, mais pour qu’ils ne soient pas dans la même ligne; comme le montre l’image suivante.

Cas d’arêtes se faisant face dans des lignes différentes

Cas d’arêtes se faisant face dans des lignes différentes[/caption] Si nous trouvons deux arêtes mais dans la même position (comme dans l’image suivante), nous devons appliquer cet algorithme pour le résoudre: (R, U, R', U') F', U, F

Cas d’arêtes se faisant face dans la même ligne

1. Nous avons deux bords qui se font face, mais pour qu’ils ne soient pas dans la même ligne, c’est-à-dire situés à droite et à gauche. Dans ce cas, nous effectuerons l’algorithme suivant: (R, U, R', U') F', U, F.

Les bords sont dans la bonne position pour la résolution. C’est-à-dire l’un devant l’autre mais dans des lignes différentes.

Les premiers bords.

Les premiers bords sont les plus faciles à résoudre.

Nous allons commencer par placer le cube dans une position de référence, afin qu’il soit plus confortable à déplacer. Notre position de référence sera le blanc face vers le haut et le jaune vers le bas. De cette façon, les bords que nous allons résoudre seront horizontaux pour nous dans le reste des faces du cube.

Pour commencer, nous garderons les bords que nous faisons sur le visage blanc et jaune. Cette partie est la plus simple et deviendra progressivement plus compliquée.

Nous plaçons les bords dans le cas que nous avons précédemment expliqué qui nous intéresse, l’un devant l’autre mais dans des lignes différentes; nous les assemblons et montons à l’étage pour économiser. Nous procéderons comme suit :

• Pour rejoindre, nous n’aurons qu’à tourner les deux couches supérieures ou inférieures d’un côté.
• Pour grimper, nous tournons la couche extérieure à droite ou à gauche (selon l’endroit où nous avons le bord) vers le haut; nous protégeons le mouvement et redonnons.

Cela dépend de l’endroit où nous gardons l’avantage, nous effectuerons un algorithme ou un autre:

À droite : Uw', R, U, R', Uw.

Gauche : Dw', L', U, L, Dw

Dans l’image suivante, nous vous montrons un exemple de ce que ce serait si nous enregistrions le bord à droite avec l’algorithme Uw', R, U, R', Uw

Nous allons répéter ces mêmes mouvements jusqu’à ce que nous fassions toute la couche du centre blanc avec des bords que nous avons bien placés. Pour ce faire, lorsque nous montons, nous devons toujours essayer d’abaisser un bord mal fait.

Lorsque nous avons la couche supérieure avec le centre blanc avec quatre bords corrects, nous tournons le cube. e forma, maintenant la couche du centre jaune est au-dessus et celle du centre blanc en dessous.

Nous continuerons à faire des bords comme nous l’avons expliqué et à les placer dans la couche supérieure (dans ce cas le centre jaune). Ne vous inquiétez pas de démonter le cube, car les bords que nous continuerons à chercher dans les couches centrales, nous ne casserons pas ce que nous avons déjà fait.

Lorsque vous terminez les bords de ce calque, la chose la plus compliquée commence. Maintenant, détendez-vous. Faites-le tranquillement, prenez votre temps pour chercher les pièces dans la position qui vous intéresse et allez placer les bords et, surtout, n’abandonnez pas. Tout est une question de pratique.

Les bords centraux

Pour résoudre les bords centraux, nous devons abaisser l’un des bords que nous avons faits au centre du cube, afin que nous puissions continuer à faire des bords comme nous l’avons généralement fait et à les placer au-dessus. Nous n’aurons à faire cette étape que deux fois; les deux derniers bords seront soit faits, soit faits d’une autre manière.

Les deux derniers bords nous seront soit donnés, soit nous devrons les terminer d’une autre manière.

Dans ce cas, si les deux derniers bords ne nous ont pas été donnés par nous aurons deux cas:

• Dans le premier cas, les bords se font face en différentes lignes. À cette occasion, contrairement au reste du processus, cela ne nous intéresse pas.
• Dans le second cas, nous aurons les deux bords face à face. C’est ce que nous rechercherons.

Si la situation du premier cas apparaît, nous devrons appliquer l’algorithme de retournement que nous avons appliqué à ces occasions, et qui est expliqué ci-dessus. Répétons-le encore une fois :

Avec les deux bords situés à notre droite et à gauche: R, U, R', U') F', U, F.

En faisant cet algorithme, nous obtiendrons le deuxième cas, c’est-à-dire que nous aurons deux bords face à face (celui qui nous intéresse à cette occasion). Rappelez-vous que pour les mettre face à face, vous pouvez, si nécessaire, tourner les couches extérieures. Ces mouvements ne supposeront aucun changement et ne briseront aucun centre ou bord déjà fait.

Lorsque nous aurons réussi à mettre un bord face à l’autre, nous appliquerons un algorithme que nous connaissons déjà et nous les aurons tous prêts. Préparé? Allons-y!

Nous devrons diviser les deux couches supérieures en faisant Uw, puis appliquer l’algorithme de retournement; enfin on retourne le mouvement des couches supérieures et... Voilà. L’algorithme est (avec les deux arêtes situées à notre gauche et à notre droite): U’w, (R, U, R', U') F', U, F, Uw.

Résolution 3x3 avec parités

Nous avons déjà fait tous les centres et tous les bords. Vient maintenant la partie la plus facile et la plus amusante, car nous n’aurons qu’à résoudre le cube comme un 3x3 normal et nous aurons terminé notre cube 4x4.

Cependant, au cours du processus, nous pouvons rencontrer quelques problèmes ... Vous remarquerez que lorsque vous faites la croix jaune, vous n’obtenez pas les pièces être placés dans leur position correcte. Très simple, vous êtes face à un cas de parité ! Mais pas de panique... ci-dessous, nous expliquerons ce que vous devez faire pour le résoudre.

Revenons au début de cette partie et recommençons :

Lorsque nous avons déjà les centres et les bords faits de notre rubik’s cube 4x4, nous devons imaginer que notre cube est un 3x3. Vous savez comment résoudre un 3x3, n’est-ce pas? Eh bien, appliquez vos algorithmes pour faire la croix blanche, puis placez les coins, puis les bords centraux et, enfin, faites la dernière couche. Puits... peut-être que votre méthode est d’une autre manière, faites-le comme vous le savez et ce sera plus confortable pour vous!

Lors de la création de la dernière couche, il peut y avoir quatre cas:

1. CAS 1 : RÉSOLU

Dans le meilleur des cas, vous pouvez faire et finir votre cube sans problème. Si c’est votre situation... Félicitations, vous avez déjà terminé votre 4x4 et vous n’avez pas trouvé de parité! Si ce n’est pas le cas... Lire.

2. CAS 2 : PARITÉ DE L’OLL

Vous faites la croix jaune et vous trouvez un bord qui est retourné. Vous avez trouvé la parité OLL ! Lorsque nous faisons la croix jaune sur un 3x3 nous trouvons quatre cas: la pointe, un bord, la ligne et un L, communément appelé « Las 9 ». Eh bien, si vous voulez reconnaître le premier si nous allons devoir effectuer un algorithme OLL dans notre 4x4, faire la croix jaune sera orientée ou une seule arête ou le L; c’est-à-dire un nombre impair d’arêtes orientées.

Pour résoudre le cas de parité en même temps que vous le voyez, utilisez l’algorithme de parité OLL. Quel que soit l’bord par lequel vous commencez à appliquer l’algorithme, il sera supprimé partout où vous le faites; mais l’optimal serait que vous commenciez sur le bord qui a la parité. L’algorithme est le suivant :

Parité OLL: Rw, U2, (x) Rw, U2, Rw, U2, Rw' U2, Lw, U2, Rw' U2, Rw, U2, Rw' U2, Rw'

Exemple de parité OLL

3. CAS 3 : PARITÉ PLL

Vous trouvez deux pièces échangés ensemble. Cela signifie qu’il a deux bords bons et deux mauvais. Encore une parité ! Cette fois, c’est le PLL et est plus facile à résoudre que le précédent.

On peut aussi bien trouver tous les bords et deux coins mal. Ne vous inquiétez pas, il est résolu avec le même algorithme.

En conclusion, vous aurez deux pièces échangés ensemble, soit des bords ou des coins; et l’algorithme avec lequel il est résolu est le suivant.

Parité PLL : r2, U2, r2, Uw2, r2, Uw2  

Exemple de parité PLL

4. CAS 4 : DOUBLE PARITÉ

Le dernier cas que nous pouvons trouver sera celui dans lequel les deux types de parités apparaissent ensemble; celle de l’OLL et de la PLL. Ne vous inquiétez pas, les algorithmes sont les mêmes que ceux que nous venons d’apprendre et exécutés dans l’ordre suivant:

Tout d’abord, l’OLL est fait parce que ce sera celui que nous verrons en premier et, enfin, le PLL. Une fois les deux algorithmes exécutés, nous allons résoudre le cube par notre méthode habituelle.

Nous avons déjà fait notre 4x4!!. Maintenant, vous n’aurez plus qu’à pratiquer beaucoup et bientôt vous le résoudrez sans problème.

Avez-vous trouvé cela difficile? Si vous préférez, vous pouvez compter sur nos tutoriels vidéo. Nous y expliquons tout ce qui est lu ci-dessus.

Vidéo pour résoudre les rubik’s cube 4x4

Vidéo pour résoudre les parités

Et... Si vous avez encore des questions après avoir lu le tutoriel et regardé les vidéos, écrivez-nous un commentaire et nous essaierons de vous répondre dans les plus brefs délais.

Résolvez-le!